GaN HEMTエンハンスメント型デバイスの開発について（２）

はじめに

前回は，AlGaN/GaN HEMTを高速・高電力なスイッチング電源回路に使用するための，エンハンスメント型デバイスについての技術を見てみました．また，MISゲート構造を用いた，AlN/GaN MIS-HEMTエンハンスメント型のモデルに改造するための基本的な物理式の導出を行いました．
今回はMIS-HEMT構造デバイスのモデル化の続きとして，バイアス依存ドレイン・ソース抵抗と自己発熱のモデルを考察したいと思います．

AlN/GaN MIS-HEMTのドレイン・ソース抵抗モデル [1]

ドレイン抵抗 (RD) とソース抵抗 (RS) はゲートのフィンガー数（N_GF）に依存して増加します．これはMOSFETなどと同様です．つまり，

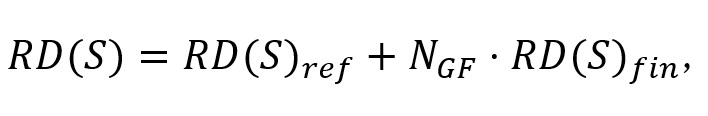　(1)

ここでRD(S) _ref は正規化したドレイン (ソース) 抵抗で，RD(S) _fin はそれぞれのゲートフィンの寄生抵抗になります．
式(1)は測定データによるフィッティングモデルとしては正しいですが，物理的に考えると，ドレイン（ソース）抵抗はバイアス電圧に依存しないシート抵抗とコンタクト抵抗，バイアスに依存して変化するアクティブ抵抗成分に分けられます．バイアスに依存しないドレイン抵抗（rd_fix）とソース抵抗（rs_fix）はデバイスの温度（T_dev）と環境温度（T_nom）に依存しています．ここでRCD(S) をドレイン（ソース）のコンタクト抵抗とすると，これらはN_GF とW_eff に反比例して以下のようにあらわせます．

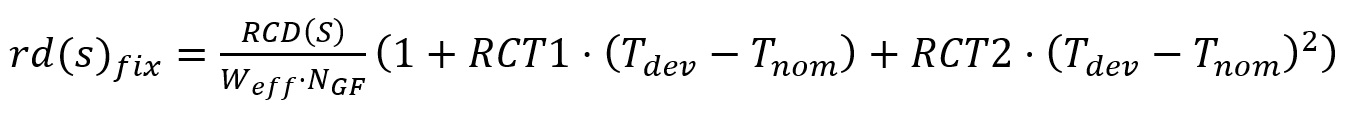　(2)

ドレイン・ソース抵抗は外部抵抗で非対称です．これによって正確なRF／パワーMISFETのシミュレーションが可能になります．バイアス依存のドレイン・ソース抵抗は外部抵抗ノードと内部ノードの間に接続されます．ゲートバイアス依存のドレイン・ソース抵抗はrd_fix と rs_fix とおいて，

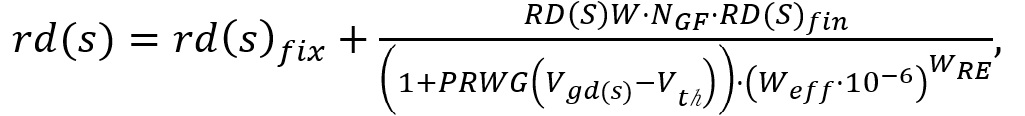　(3)

ここでRD(S)W は単位ゲート幅のドレイン（ソース）抵抗です．PRWG は能動抵抗のパラメータで，W_RE はゲート幅によるスケーリング係数です．

実際のAlN/GaN MIS-HEMT測定データを用いて，以上のモデル式をVerilog-Aモデルに作成しパラメータを抽出しました．図１，２により，ゲート電圧が大きく変化した場合でも，ドレイン電流特性が追従することが観察できます [2]．

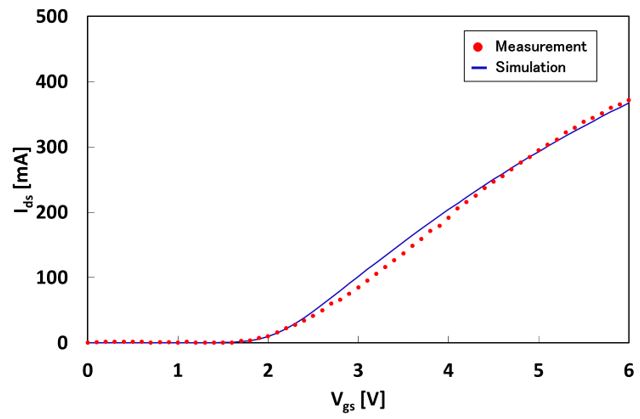
図１．線形領域におけるIds-Vgs特性の例 (V_ds = 100 mV) [2].

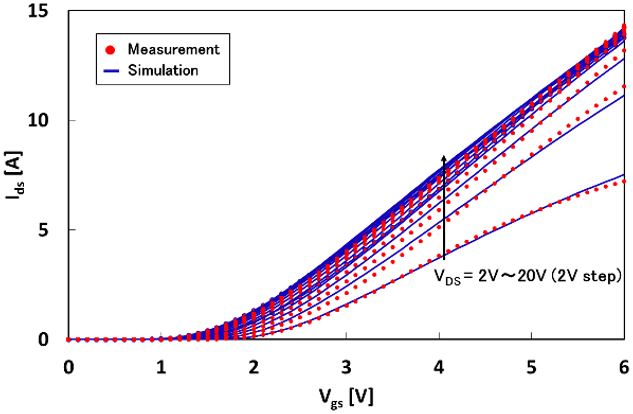
図２．飽和領域におけるIds-Vgs特性の例(Vds = 2V~20V) [2].

自己発熱モデル

自己発熱現象については，ユニポーラ，バイポーラトランジスタに限定されず電流が流れる経路において，周りが温度遮蔽物（絶縁物など）で囲まれている部分で発生します．電流が多く流れると抵抗成分によってジュール熱が発生するため，温度上昇がおこります．すると，デバイス自体の温度が上昇し，電気特性がその温度によって変化します．
自己発熱モデル自体は，今回取り上げたGaN HEMT独自のものではありません．しかし，MIS-HEMT構造デバイスにおいては，ゲートに絶縁膜を入れているため自己発熱が起こりやすくなっています．

熱サブ回路による自己発熱モデルの問題点 [3]

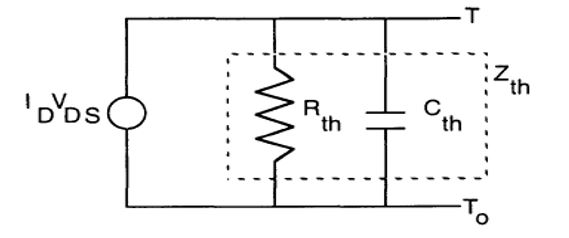
図３．従来の熱サブ回路による自己発熱モデル．
ここでZ_th は熱インピーダンスでI_D はドレイン電流，V_DSはドレイン・ソース電圧．

HEMTやMOSFETなどのユニポーラトランジスタの自己発熱は，チャネルに流れる電流によってジュール熱が発生して，デバイスの温度の上昇により流れる電流が減少してしまう物理効果です．特に大きな電流を扱うデバイスのシミュレーションでは，モデル化が必要です．

自己発熱現象を表すSPICEモデルは，図３のような熱サブ回路による手法が一般的です．サブ回路として定義される熱等価回路は、シリコンオンインシュレータ (SOI) MOSFET，バイポーラ接合トランジスタおよび横方向拡散 MOSFET (LDMOS) モデルで広く使用されています．デバイスに内部温度ノードTを定義することで自己発熱が影響します．このノードは，熱抵抗R_thと容量C_th のネットワークを介して低電圧ノード T₀ に接続されており，T₀ のノード電圧は実際にはデバイスの温度です．SPICE エンジンは，デバイスの物理ノードと温度ノードの両方で収束基準が満たされるまで，ニュートンラフソン反復を実行します．反復のため，自己発熱モデルを使用した複数のトランジスタを含む大規模な回路シミュレーションでは，収束の問題がしばしば発生します．以前筆者らは，このモデルを用いたBSIMSOIモデルで形成した51段SOI n-MOSFETリングオシレータが，時間領域シミュレーションで収束できない現象を確認しました．

等価回路を用いない自己発熱モデル [4]

Verilog-Aによるコンパクトモデルでは，上記熱サブ回路による手法を用いても，以前より収束するようになってきたようですが，方程式のみによる手法は，やはり収束スピードが高速であることが確認できました．そこで，以下にその原理を説明します．

直流電流とイソ・サーマル電流の関係は以下のようになります．

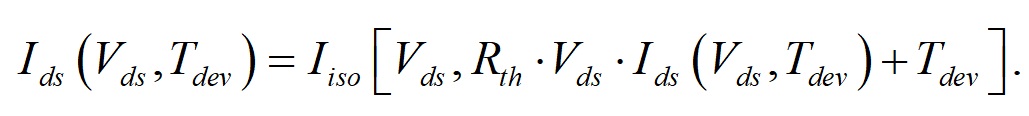　(4)

自己発熱によるチャネルの温度上昇は，

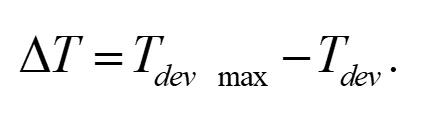　(5)

ここで， T_{dev_max} はチャネルの最高温度で，T_dev は環境温度です．DT は以下のように定義できます．

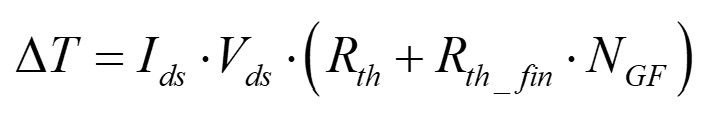　(6)

R_th は係数R_{th_fin},に比例して増加します.

完全な熱発生の流れを求めるには，トランジスタの構造を３次元で計算する必要があります．しかしここでは，閉じた箱の中で相対的な温度上昇を得られれば良いので，長方形の材料を想定し線形方程式を解くことにします．

R_th は電気抵抗の式によって以下のようになります．

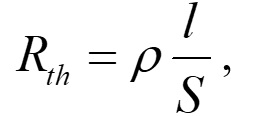　(7)

そしてその温度依存は，

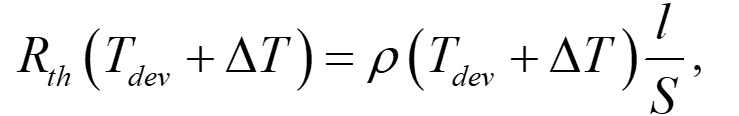　(8)

ここで ρ は熱低効率，l は実効長，S はサンプル材料の断面面積になります．ρ は温度上昇に正比例するので，以下のように表せます．

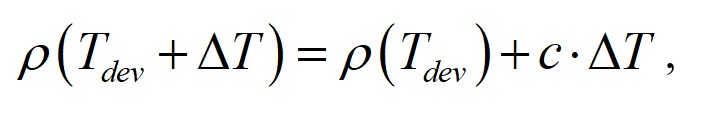　(9)

ここで，c はρ - Tの傾きです．式（9）を式（8）に代入すると，

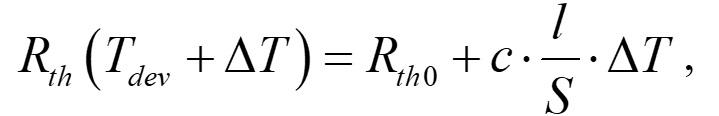　(10)

ここで，R_th0 は環境温度における熱抵抗です．K_th は以下のようになります．

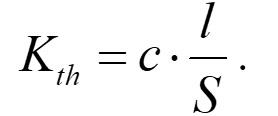　(11)

式（10）と（11）を使って，R_th は以下のような単純な式で表せます．

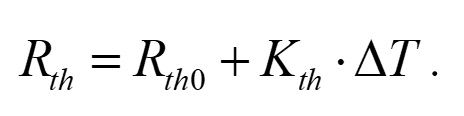　(12)

ここで，K_th はフィッティング・パラメータとして使用します．交流解析においては，熱容量 C_th はR_thに接続されます．そこで，熱インピーダンスZ_thは式（6）により以下のように表せます．

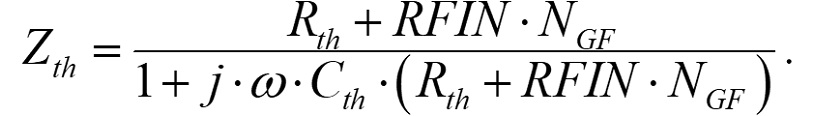　(13)

式（6）は以下のように書き直せます．

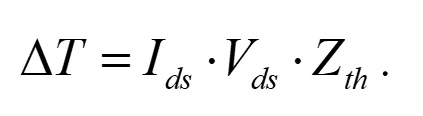　(14)

自己発熱を伴ったドレイン電流I_{ds_th}を求めるには，まず，実効移動度による温度依存を導出する必要がありますが，MOSFETなどと同様に以下のように定義できます．

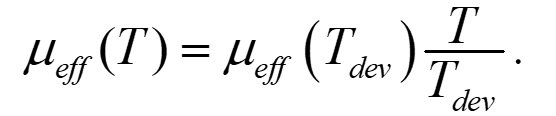　(15)

自己発熱を伴う実効移動度は，以下のようになります.

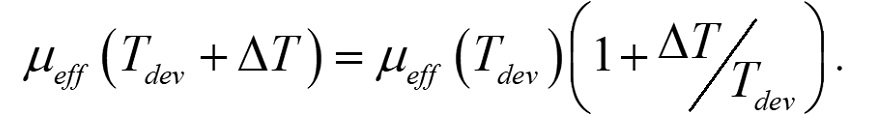　(16)

よって, 自己発熱によるドレイン電流式は以下のように書けます．

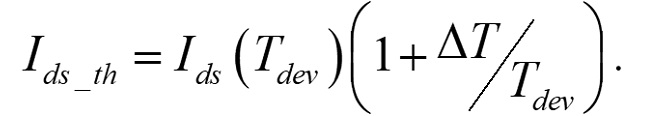　(17)

以上の式は物理的であるにもかかわらず単純であるため，直接Verilog-Aのモデル式に使用できます．

図４は図１，図２と同じデバイスの測定データを用いて，飽和領域におけるI_ds-V_ds特性を比較したものです．V_dsが高くなる領域で自己発熱現象が表れており，測定とシミュレーションが合致しています [2]．

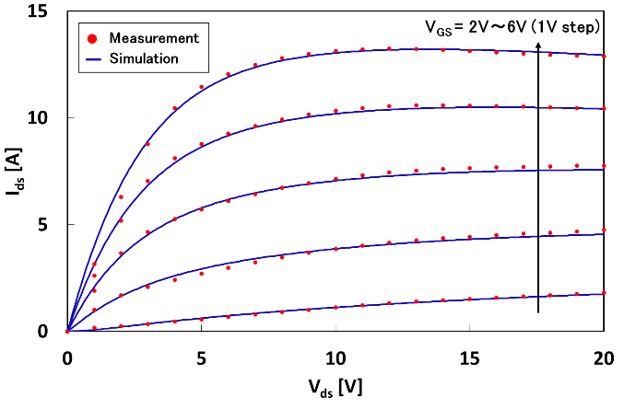
図４．飽和領域におけるI_ds-V_ds特性の例 [2].

まとめ

今回はMIS-HEMT構造デバイスのモデル化の続きとして，バイアス依存ドレイン・ソース抵抗と自己発熱のモデルを考察しました．モデルを搭載したシミュレータを用いて，AlN/GaN MIS-HEMTの実測値とモデルの比較例も示しました．
次回はMIS-HEMT構造デバイスの小信号等価回路について考察します．また，MIS-HEMTデバイスの問題点についても言及します．

参考文献

H. Aoki, H. Sakairi, N. Kuroda, Y. Nakamura, K. Chikamatsu, and K. Nakahara, “A Small Signal AC Model Using Scalable Drain Current Equations of AlGaN/GaN MIS Enhancement HEMT,” 2018 Radio Frequency Integrated Circuit Symposium (RFIC2018) at International Microwave Symposium, Philadelphia, PA, U.S.A.
H. Aoki, N. Tsukiji, H. Sakairi, K. Chikamatsu, N. Kuroda, S. Shibuya, K. Kurihara, M.Higashino, H. Kobayashi, and K. Nakahara, “Electron Mobility and Self-Heat Modeling of AlN/GaN MIS-HEMTs with Embedded Source Field-Plate Structures,” 2016 IEEE Compound Semiconductor IC Symposium, Oct. 23-26, 2016, Austin, Texas, U.S.A.
Y. Cheng and T. A. Fjeldly, “Unified Physical I-V Model Including Self-Heating Effect for Fully Depleted SOIMOSFET’ s,” IEEE Trans. Electron Devices, vol. 43, pp. 1291-1296, Aug. 1996.
H. Aoki and H. Kobayashi, “Self-Heat Characterizations and Modeling of Multi-finger n-MOSFETs for RF-CMOS Applications,” IEEE Trans. Electron Devices, vol. 62, Sep. 2015.

（株）モーデックでは，高度なVerilog-Aを含むコンパクトモデル開発，測定，パラメータ抽出システム開発など，モデリングに関する様々なご依頼をお受けいたしております．いつでもお気軽に問い合わせください．

第11回 GaN HEMTエンハンスメント型デバイスの開発について（２）