はじめに
前回の記事では,GaN HEMTの経験的なコンパクトモデルについて,Angelov GaN-HEMTモデルを挙げて紹介しました.
今回は,物理的モデルの一つとして,Advanced SPICE Model for HEMTs(ASM-HEMT)モデルをみてみます.
化合物半導体の物性を基本としたコンパクトモデル
前回言及したように,化合物半導体の物理現象を完全に解析してコンパクトモデルにすることは非常に困難であるため,物理的なモデルと言われているモデルであっても,基本的な電流式や小信号等価回路などを導出して,実デバイスの測定結果に基づき数学的な関数によって半経験的な手法を用いることが行われています.
コンパクトモデルに物理モデルが要求される理由を振り返ってみると,
- プロセス開発で求めたプロセスパラメータ値を,ほとんどそのままコンパクトモデルに使用したい
- デバイス構造を改良する際に,プロセスパラメータを変更して電気特性などを予想したい
- インスタンス(ゲート長・幅,膜厚,温度など)パラメータの変更で,デバイスの電気特性が実測と近いものとなるので,回路設計時に様々なサイズのデバイスを使用してシミュレーションしたい
などが考えられます.
以上のような要求は,完全な物理モデルでなくても上記の半経験的なモデルで解決できます.どのコンパクトモデルも“物理的”と言っているのは,物理ベースということで,その度合いは様々ですが半経験的であるといえるでしょう.特に化合物半導体のモデルでは経験的度合いが高いと思います.
フィールドプレート構造
元々絶縁破壊電界が高いGaNの特徴を最大限生かすために,ゲート電極がドレイン電極側にせり出した形状(ゲート・フィールドプレート:GFP)は良く用いられる方法の一つです.電界集中を緩和することはFET耐圧を向上させるために有効な手段となります.密となっていた領域の電位分布が広がり電界集中が緩和します.これをGaN層チャネル領域の電界強度分布として示したのが図1です.
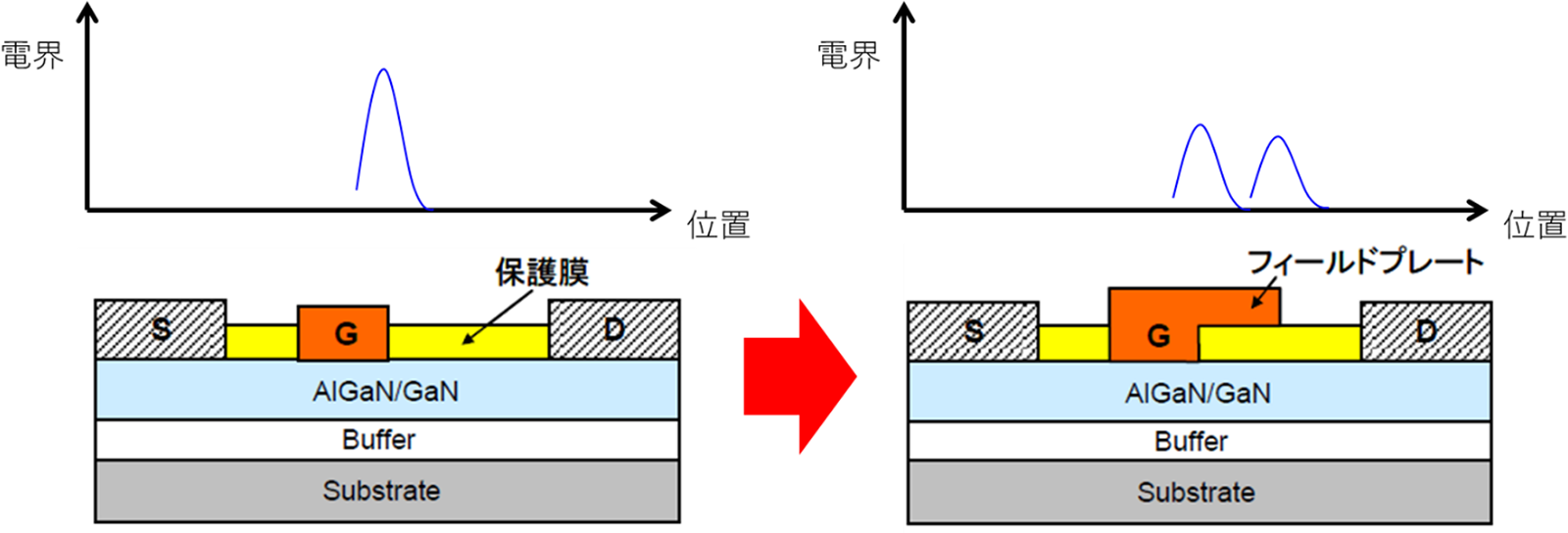
図1.GaN HEMTのGFP技術適用時における電界の変化
しかし,ゲート・ソース容量が増加してしまうため,周波数特性が劣化してしまうという問題もあります.ゲート・ドレイン間にソース電極と同電位のフィールドプレート(ソース・フィールドプレート:SFP)電極を設置する手段も使われています.図2のように,ゲート・ドレイン間にソース電極と同電位のSFP電極を設置します.
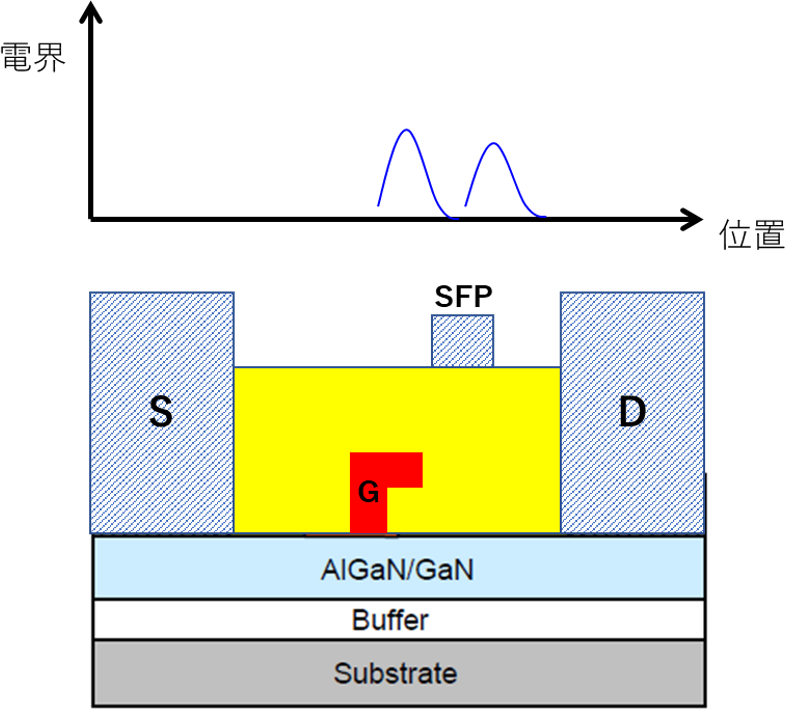
図2.GaN HEMTのSFP技術適用時における電界
ゲート電極上にSFP電極が被覆されているとゲート・ソース間容量が増加しますが,最大電界強度は低減します.SFP電極のドレイン端位置は固定し,SFP電極の長さを変更して,ゲート電極からの距離を離せば,ドレイン・ソース容量は増加しますが,FETの動作周波数への影響は回避できることが判明しています.
ASM-GaN-HEMTモデルや,次回言及するMVSGモデルではGFP,SFPの効果がサポートされています.
ASM-GaN-HEMTモデル
ASM-GaN-HEMTはGaN HEMT用の高度な物理ベースのSPICEモデルとして開発されました.モデルの構造として3つの部分に分けられます.
- 表面電位式と基本チャネル電荷式
- 基本端子電流および電荷モデル
- デバイス内の経験的デバイス効果のモデル
このように1および2部分が物性ベースで導出されており,3が数学的な関数式でできています.
本記事では,本モデルの特徴ともいえる1について着目し,さらにフィールドプレートのモデルの考え方を言及します.詳細については文献[1]を参照してください.
図3はAlGaN/GaN HEMTの代表的な構造です.
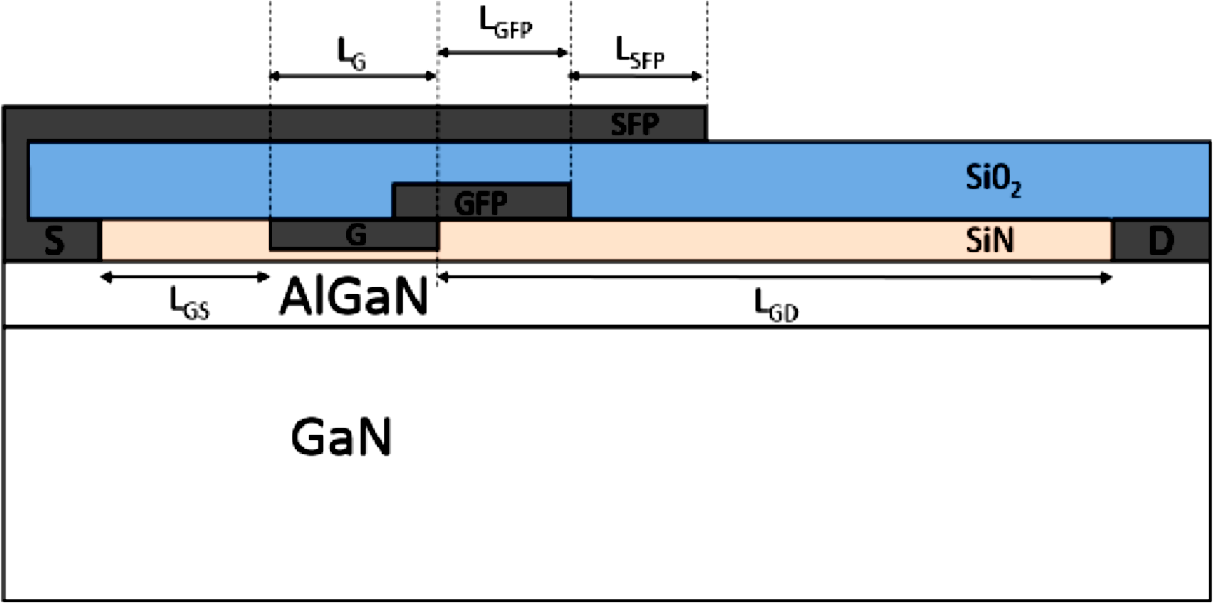
図3.AlGaN/GaN HEMTの簡易的構造 [1]
表面電位計算 [1]
2次元電子ガス(2-DEG)の物性は,HEMTデバイスの動作の中核であり,物理的に導出することは重要です.最初に,2-DEG電荷密度の物理ベースのモデルの開発に焦点があてられました.2-DEG電荷密度をモデル化する際の主な課題は,いかにして簡単な方程式で表現するかということです.最も困難なのが量子井戸のnsによるフェルミ準位Efの変化の導出です.シュレディンガー方程式とポワソン方程式をAlGaN/GaN HEMTに適用した場合のキャリア統計は,超越方程式(Transcendental equation)に展開されます.コンパクトモデリングでは,数値に基づく方程式であるため解析的な解法を使用しています.様々な領域において,ゲート電圧に対するEfを分割してnsを解析的な手法で求めています.これらの領域は物理的に意味があり,エネルギー準位E0とE1のEf対する位置に基づいています.これはすべての領域で導出され,全領域で統一された式で表しています.実際に表面電位計算は,以下のように導出されています.
ゲート電圧による表面電位の変化は,
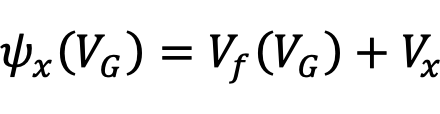 (1)
(1)
ここで,Vfは三角形の電位壁におけるフェルミレベルを基準とした電位で,Vxは表面電位を算出する電圧ポイントです.Vfの計算は,ヘテロ接合を三角形の電位壁と仮定した場合,シュレディンガー方程式を解くと,エネルギーサブバンドの位置が得られます.
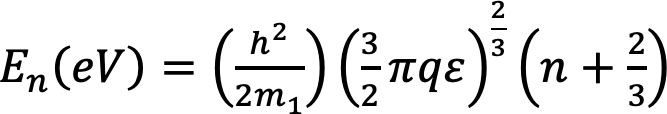 (2)
(2)
ここで,eは三角形電位壁を交差する電界,nは任意の整数,m1は三角形電位壁での実行電子数,hはプランク定数を表します.エネルギーレベルの下位2つのサブバンドは,
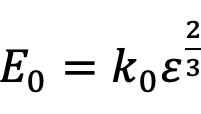 (3)
(3)
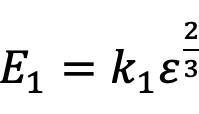 (4)
(4)
であり,ポアソン方程式を解くと以下のように電界とシート電荷密度の関係が得られます.
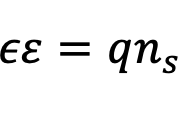 (5)
(5)
式(5)を式(3)と(4)に代入すると,
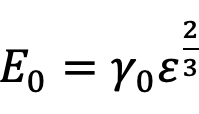 (6)
(6)
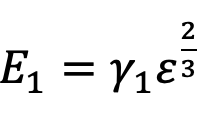 (7)
(7)
ここでフェルミディラック統計モデルを適用すると,
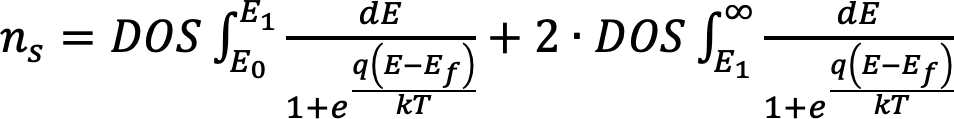 (8)
(8)
ここで,DOSはGaN内の2次元順位密度です.積分を行うと,
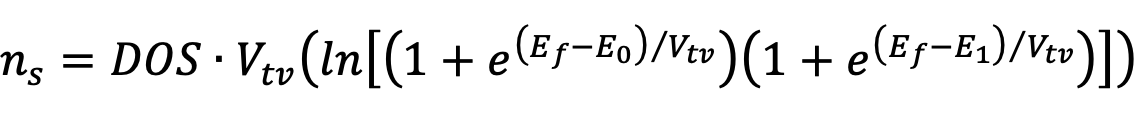 (9)
(9)
ここでAlGaN層が完全にイオン化しているとすると,電荷均衡状態なので,
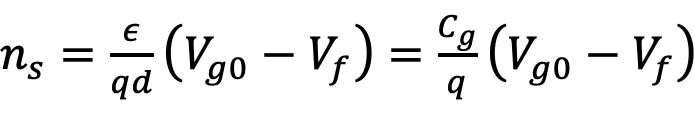 (10)
(10)
ここで,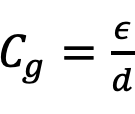 です.式(6)から(10)を超越方程式により解いて,各サブバンドとVfの条件によってVGの依存を求めれば,動作領域別のVfが求まるというわけです.この計算は,非常に込み入っているため,ここでは割愛します.
です.式(6)から(10)を超越方程式により解いて,各サブバンドとVfの条件によってVGの依存を求めれば,動作領域別のVfが求まるというわけです.この計算は,非常に込み入っているため,ここでは割愛します.
フィールドプレートモデル(GFP, SFP)
先に述べた,GFPとSFPのモデルは,図4のようなマクロモデルとしてVerilog-Aのコードで記述されています.本モデルは,文献[2]を最近入れたようですが,次回言及するMVSGモデルが先行しています.
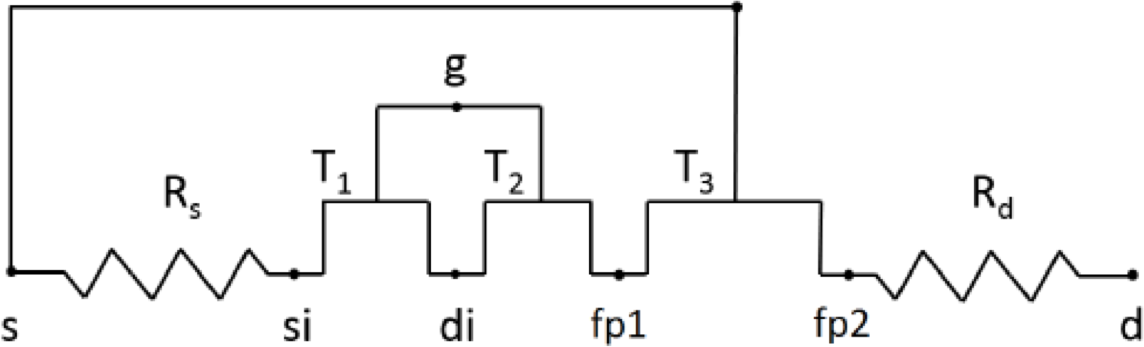
図4.AlGaN/GaN HEMTのゲート,ソース・フィールドプレート付きマクロモデル [2]
考え方としては,フィールドプレートをサブトランジスタと考えて,主トランジスタのモデルを各端子の接続によってシミュレートするものです.そのため主トランジスタのモデル式のパラメータを割愛して作成されています.また,図4のRs, Rdについては,ゲート電圧依存の可変抵抗となっており,Rs, Rdのモデル式にあるパラメータを調整することで,フィールドプレートモデルのパラメータが正確でなくても,ある程度十分な電気特性が得られます.
まとめ
今回は,物性を元に半経験的に開発されたモデルについて紹介し,Advanced SPICE Model for HEMTs(ASM-HEMTモデル)を見てみました.主に表面電位計算による量子井戸のnsによるフェルミ準位Efの変化の導出を紹介しました.また,AlGaN/GaN HEMTで耐圧を上げるためのプロセス技術,フィールドプレート構造とASM-HEMTモデルでの搭載についても言及しました.詳細については,文献[1-2]などを参照してください.
次回はもう一つの物理ベースのCMC推奨モデル,MVSGモデルを紹介します.
参考文献
[1] S. Khandelwal, “Compact modeling solutions for advance semiconductor devices, " Ph.D. dissertation, Norwegian University of Science and Technology, 2013.
[2] S. A. Ahsan, S. Ghosh, K. Sharma, A. Dasgupta, S. Khandelwal, and Y. S. Chauhan, “Capacitance Modeling of a GaN HEMT with Gate and Source Field Plates,” IEEE International Symposium on Compound Semiconductors (ISCS), Santa Barbara, USA, June 2015.
(株)モーデックでは,高度なモデル開発,測定,パラメータ抽出システム開発など,モデリングに関する様々なご依頼をお受けいたしております.いつでもお気軽に問い合わせください.

